CCB KW ECDSA Signature STM32U3 How to Introduction


Introduction article for Coupling Chaining Bridge example with Key Wrapped for an ECDSA Signature


Step by step article: How to start with CCB KW ECDSA Signature

Literature


Introduction

The protection of the private key is critical for the security of asymmetric cryptography.
The Coupling and Chaining Bridge (CCB) hardware feature embedded in the STM32U3 is used to protect this private key.
The CCB is used to wrap the key. It ensures that even the application can't access to this secret key in clear.
Furthermore, the wrapped key is only valid for a specific device.

The proposed step by step example shows how to practically wrap the key and how this wrapped key is used without exposing it in clear.
The example shows how to perform a message signature using a wrapped private key and how to verify this signature using a public key.
The digital signature solution used in this example is the ECDSA algorithm (Elliptic Curve Digital Signature).

The ECDSA algorithm requires a "nonce", important for the ECDSA security and generated for every new ECDSA signature.
This nonce is a random number generated by the hardware Random Number Generator embedded in the device and The generation of this random number is also protected through the CCB feature.


1. MbedTLS_HW_KWE

The described "How to" is based on the MbedTLS_HW_KWE example provided in the STM32Cube_FW_U3.
MbedTLS is an open-source C library for cryptography (TLS Transport Layer Security: protocol for secure communication over a computer network).
This open-source cryptography library is adapted by ST to be used for STM32 devices and provided in the STM32Cube_FW.
For the key wrapping using the CBB, a dedicated library has been created (MbedTLS_HW_KWE).

2. Digital signature

To understand the proposed example, some background about digital signature is needed and specially ECDSA (Elliptic Curve Digital Signature).

  • A digital signature guarantees the authenticity of a digital content. In other words, the author/sender is the right expected one. Furthermore, the sender who has signed it can’t deny they are the author (non-repudiation).
  • The integrity of the digital content needs also to be guaranteed to ensure that the signed document has not been modified.
  • Typical STM32 use cases:
    • Verify the authenticity of an STM32 device before installing a firmware.
    • Verify the authenticity and integrity of a FW before installing it on a die.
  • Digital signature uses asymmetric cryptography => a pair of key (one public, one private).


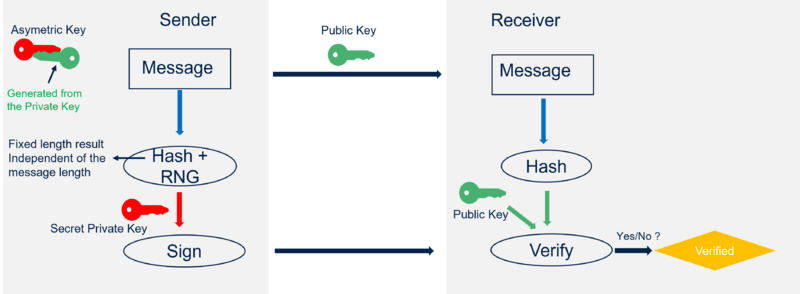
Figure 1. Digital signature and signature verification

The figure above shows the principle to generate a signature of a message and how it is verified.

  • Sender
    • A HASH (e.g. SHA2) algorithm is used to create a fixed length digest from the message. This solves also the issue if the message is very short or very long.
    • To reuse a private key to generate several signatures, it is important to add a random number that every generated signature is different.
    • The signed result is sent to the receiver together with the message in clear, the public key and all the parameters of the used signing algorithm.

Notes:

  • The only secret is the private key and the random number, all the rest is public. It shows that the protection (role of the CCB) of this private key and RNG is crucial.
  • The public key is the only one that can be used to verify the signature.
  • Receiver
    • The receiver computes the hash of the message (sent in clear) and use the hash result for the ECDSA algorithm.
      • If the public key allows to verify the signature, it proves the authenticity and integrity of the message.

Understanding the principle of a digital signature is already enough to execute the "how to" example.
But a detail analysis and understanding of the provided CubeFW example requires some know-how about the ECDSA algorithm.


3. To learn more about the Elliptic Curve Digital Signature (ECDSA)

Refer to following articles:



Retrieved from "https://wiki.stmicroelectronics.cn/stm32mcu/index.php?title=Security:CCB_KW_ECDSA_Signature_STM32U3_How_to_Introduction&oldid=69961"